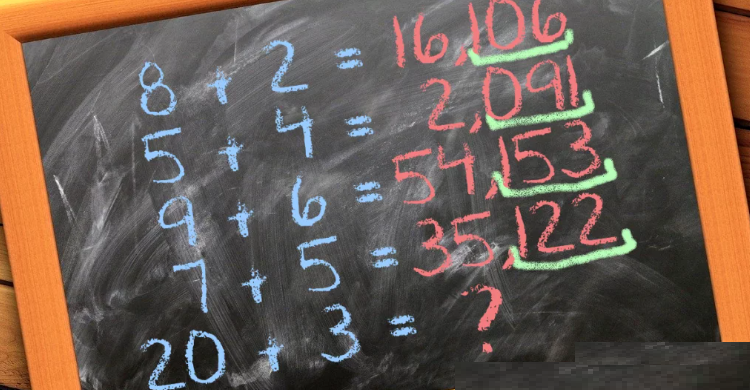Seuls les vrais génies arriveront à résoudre ce casse-tête mathématique
La série de calculs que vous voyez ici a été partagée plus de 100 000 fois et a fait craquer bien des neurones. Pour cause, elle défie les lois arithmétiques habituelles. Selon certains internautes, il faut un QI très élevé pour trouver la solution. Alors, faites le test !
23 n’est pas la réponse
Malgré les signes « + », vous comprenez au premier regard que les équations ne s’additionnent pas. Du coup, comment trouver la réponse à la dernière ? Les débats à ce sujet vont bon train. Les uns privilégiant une méthode plutôt qu’une autre, et les autres contestant tout simplement la logique de l’énigme.
Petit indice : la suite d’équations répond à un schéma caché. Pour trouver le résultat de la dernière ligne « 20 + 3 », il faut découvrir ce schéma. Ne vous précipitez pas et prenez quelques minutes pour réfléchir… Réveillez le génie qui est en vous !
Alors, quel nombre avez-vous obtenu ? Il est clair que ce n’est pas 23. Trêve de suspense. Pour vérifier si vous êtes un érudit des équations mathématiques, voici la bonne réponse et sa démonstration.
[quads id=4]
Trois opérations qui se suivent
Première équation. Pour comprendre comment on arrive au résultat surprenant de 16 106 pour 8 + 2, trois opérations ont été faites. Vraisemblablement, le premier nombre avant la virgule (16) correspond au premier chiffre multiplié par le second (8 x 2). Ensuite, pour déterminer les chiffres décimaux, d’autres opérations interviennent. Vous remarquerez donc que dans la décimale « ,106 », on peut isoler 10 qui est l’addition de 8 et 2. Et 6, qui en est la soustraction. Ce qui mène au raisonnement suivant :
Premier ensemble = a × b
Deuxième série = a + b
Troisième série = a – b
D’où 8 + 2 = 16,106
Ça y est, vous disposez du schéma à appliquer pour trouver la solution à l’énigme ! Maintenant, appliquons cela à chaque ligne.
Pour la proposition 5 + 4 = 2,091.
Soit 5 + 4 = (5 x 4) , (5 + 4) & (5 – 4)
5 + 4 = 20 , 9 & 1
et on devrait avoir 5 + 4 = 20,91
Oups ! A priori on a les bons chiffres. Mais alors, pourquoi la virgule est placée après le deux et non après le zéro dans le résultat proposé ? Regardons de nouveau la série d’équations.
[quads id=4]
La quatrième règle
Avez-vous compris ce qui se passe ? Il y a une règle supplémentaire pour résoudre le casse-tête : comme vous pouvez le voir sur chacune des équations, la décimale doit toujours contenir trois chiffres !
De haut en bas on a : 16, 106 | 2,091 | 54,153 |35,122
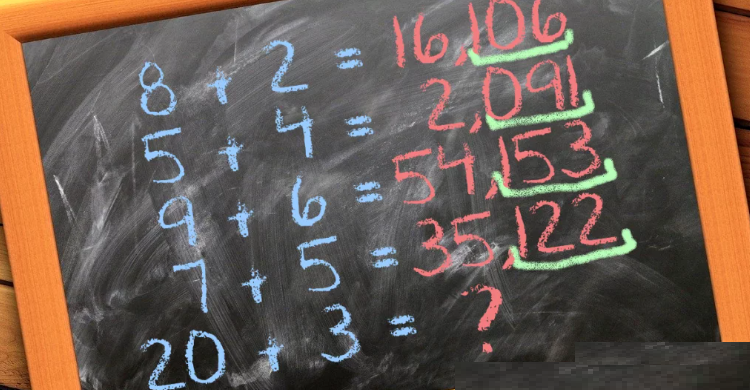
De ce fait, on inscrira 5 + 4 = 2,091 au lieu de 20,91 pour la ligne 2. Maintenant que vous connaissez toutes les règles, passons aux autres lignes.
On vous propose 9 + 6 = 54 153
Soit 9 + 6 = (9 x 6) , (9 + 6) & (9 – 6)
9 + 6 = 54 , 15 & 3
et 9 + 6 = 54,153
Passons à la suivante 7 + 5 = 35,122
Soit 7 + 5 = (7 x 5) , (7 + 5) & (7 – 5)
7 + 5 = 35 , 12 & 2
et 7 + 5 = 35,122
La solution est…
Fort de ces démonstrations, vous pouvez donc affirmer sans l’ombre d’un doute que le résultat de la dernière ligne « 20 + 3 » est 602 317.
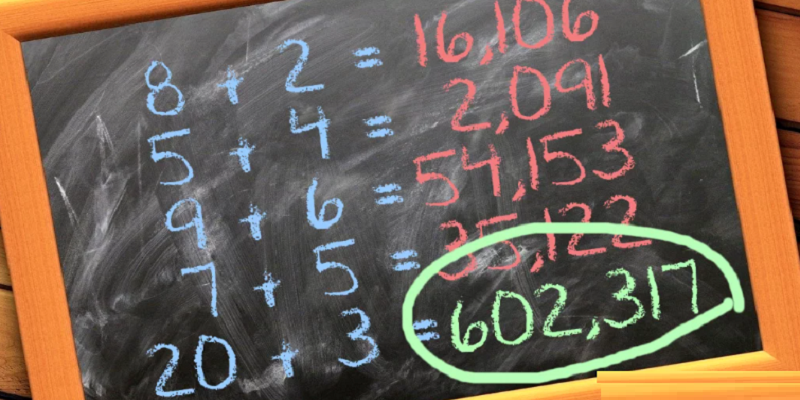
Soit 20 + 3 = (20 x 3) , (20 + 3) & (20 – 3)
20 + 3 = 60 , 23 & 17
et comme on doit avoir un résultat à trois chiffres après la virgule, la réponse finale est 602,317 !